Musings from Carbon’s Engineers

How Surface Lattices Deliver a Wider Range of Mechanical Properties

By Kyle Kloster, April 27, 2021

Latticing enables better mechanical properties

3D printing makes it possible to fabricate a wide variety of geometries that are difficult or impossible to make with legacy manufacturing processes. Lattices in particular have opened up a world of desirable mechanical properties, from better compression and energy absorption properties to lighter weight parts. Popular use cases include replacing standard foam padding with lattices having better stiffness-to-mass ratios, and using superior energy-absorption properties of some lattices to improve protective equipment like helmets and car seats.

Carbon’s Computational Geometry Team has investigated a vast parameter space of traditional strut-based lattices and novel surface lattices. Exploring this parameter space has driven innovation in lattice design and unearthed new limits to stiffness and energy absorption for consumer goods. To shed light on that discovery process, here we’ll describe some of the mathematics and engineering underpinning the surface lattices’ geometric structures, and the related analyses our parts undergo enroute to a finished product.

Latticed products with state-of-the-art mechanical properties

Learn more about the Specialized S-Works Power Saddle here.

Discover more Carbon latticing products here.

The cosmos of surface lattices

A detour with contours: 2D contour plots

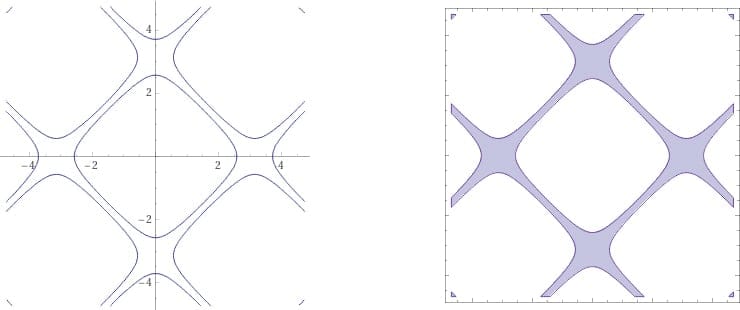
So-called “surface lattices” are 3D extensions of the familiar 2D contour plot. In contour plots,  each contour line in 2D corresponds to an “isovalue” for a function—the function takes the same (“iso”) value at every point on the contour line. For example, consider the function g(x,y) = cos(x) + cos(y). The plot below, at left, displays the contour line for the isovalue g(x,y) = 0.5. Then, plotting the inequality |g(x,y)| < 0.5 fills the space inside the contour line (below, right):

From 2D contours to 3D isovolumes

Extending that 2D case to three dimensions, instead of contour lines we have iso-surfaces, and filling the space inside the surface yields a 3D volume. Extending the function g(x,y) above to 3D yields a function that underpins the widely studied surface lattice (also called an “isovolume”) known as the Schwarz-P lattice. Pictured here, a single cell of Schwarz produced by taking the set of points inside the cubic grid [-π, π]³ where the associated function g(x,y,z) = cos(x) + cos(y) + cos(z) satisfies the inequality |g(x,y,z)| < t :

Tiling multiple copies of these unit cells together, we can build out a lattice of any shape and size to fill out a 3D model:

Popular lattices in products

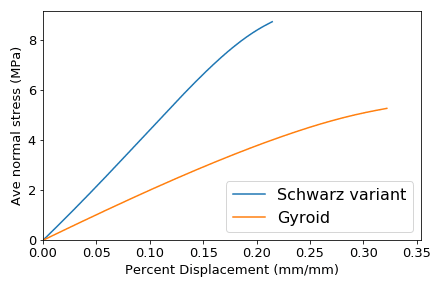
These surface lattices provide compression properties and a stiffness-to-mass ratio that make them suitable to a broad variety of applications. The interesting buckling behavior of the Schwarz lattice make it a go-to material for applications requiring cushioning, whereas the high energy-absorption of the gyroid, another popular surface lattice, make it the backbone of a number of protective pads:

Sifting through a high dimension parameter space

Applications can always benefit further from lattices with mechanical properties that are customized for the task at hand. To identify even more highly specialized lattices to meet application-specific needs, Carbon engineers work to optimize a generalized form of the isovolume functions that define the Schwarz and gyroid lattices:

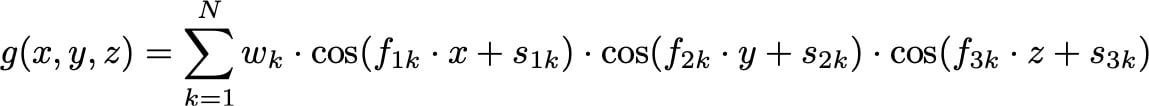
By tuning the weight (w_k), frequency (f_jk), and phase-shift parameters (s_jk) in this general form, we can produce hybrids of known lattices, zeroing in on more specifically optimized force profiles. For example, to create a relative of the Schwarz lattice with greater stiffness along one axis, we can combine the functions for the Schwarz with that of a lattice tuned for stiffness in that direction:

To craft custom lattices, we take the defining parameters for a number of suitable lattices and try blending them to achieve desired properties. Varying parameters continuously transitions smoothly from one surface lattice to the next, offering essentially an infinite space of candidates.

After generating enough of a haystack of lattices, we can organize and search through this database to find tweaked versions of promising lattices, with just enough differences to have potentially interesting and useful new mechanical behaviors. Here are some nearby neighbors of the Schwarz-P that we find in one version of the lattice database:

Evaluating lattices

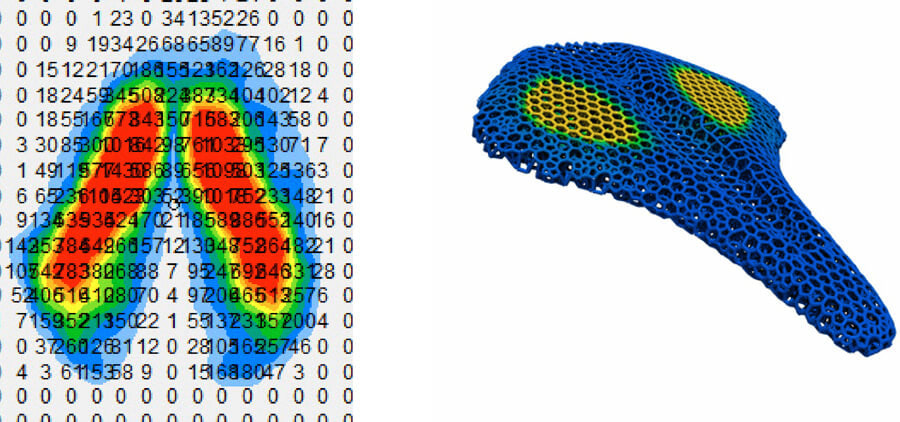
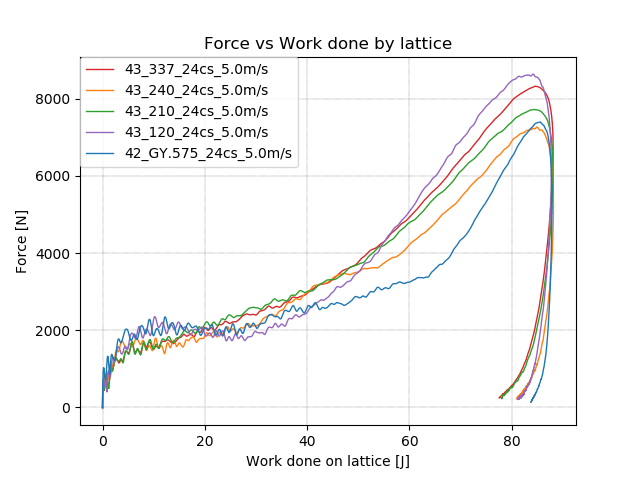
From the myriad parameter combinations we explore, we hand select a subset for further evaluation by running through our simulation software to better understand mechanical behavior like stiffness and energy absorption.

The most promising lattices continue on beyond simulations to printing and testing with physical hardware. This allows us to measure stiffness and energy absorption and return, and answer application specific questions, e.g., how well does a lattice cushion high impact blows?

The best performing pucks continue on to experimental trials within individual products. Riddell’s Speedflex helmets, powered by Carbon lattices that went through this R&D process, yielded impact reduction performance that topped the 2020 NFL testing charts.

Conclusion

The space of surface lattices contains an endless variety of mechanical properties that open up new possibilities in performance from protective and athletic equipment to medical supplies. Navigating this sea of parameters poses a rich set of complex, interdisciplinary problems; discovering new local optima in lattice space can translate into state-of-the-art products, which in turn can mean better performance and superior equipment.